A Variant of the Brillouin-Wigner Perturbation Theory with Epstein-Nesbet Partitioning 


Vol. 34,  No. 11, pp. 3279-3283, Nov.  2013
10.5012/bkcs.2013.34.11.3279


PDF
  Tumbnail

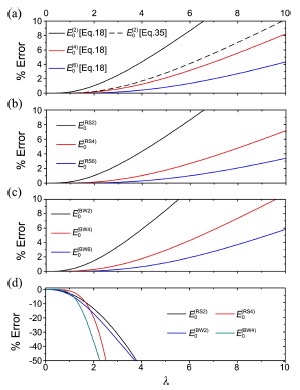
  Abstract

We present an elementary pedagogical derivation of the Brillouin-Wigner and the Rayleigh-Schrödinger perturbation theories with Epstein-Nesbet partitioning. A variant of the Brillouin-Wigner perturbation theory is also introduced, which can be easily extended to the quasi-degenerate case. A main advantage of the new theory is that the computing time required for obtaining the successive higher-order results is minimal after the third-order calculation. We illustrate the accuracy of the new perturbation theory for some simple model systems like the perturbed harmonic oscillator and the particle in a box.

  Statistics
Cumulative Counts from November, 2022
Multiple requests among the same browser session are counted as one view. If you mouse over a chart, the values of data points will be shown.


  Cite this article

[IEEE Style]

S. Lee, C. H. Choi, E. Kim, Y. K. Choi, "A Variant of the Brillouin-Wigner Perturbation Theory with Epstein-Nesbet Partitioning," Bulletin of the Korean Chemical Society, vol. 34, no. 11, pp. 3279-3283, 2013. DOI: 10.5012/bkcs.2013.34.11.3279.

[ACM Style]

Sangyoub Lee, Cheol Ho Choi, Eunji Kim, and Young Kyun Choi. 2013. A Variant of the Brillouin-Wigner Perturbation Theory with Epstein-Nesbet Partitioning. Bulletin of the Korean Chemical Society, 34, 11, (2013), 3279-3283. DOI: 10.5012/bkcs.2013.34.11.3279.

Search
(IN TITLE, AUTHOR, ABSTRACT,KEYWORDS)

Advanced Search ▼

POPULAR KEYWORDS
(TOP 10 KEYWORDS)

Recent Publications
(LAST 3 YEARS)

ISSN(Print) 0253-2964
ISSN(Online) 1229-5949